Extra Dimensions That Actually Exist
Sat Oct 22 2022
Extra dimensions! The idea of extra dimensions is a physical curiosity that science fiction writers have been enjoying for decades, and while their fanciful interpretations don’t resemble anything that really exists, it turns out there is a sense in which we actually know we’ve been living with them all along. Although rarely described this way, the extremely successful “gauge theories” of modern physics are real examples of physics that actually exists beyond the spatial directions we’re familiar with in day-to-day life. This is obviously a bold claim! To back it up, I’ll quickly explain how extra dimensions work physically, and then why it is that every fundamental force in nature lives in its own set of extra dimensions.
How do extra dimensions work?
Before tackling extra dimensions, we should be clear on what a regular dimension is in the first place. Intuitively, we’re all familiar with the fact that there are always three independent directions we can sense and move in: forward/backward, left/right, and up/down. If you boil it right down, all you ever need to know about where something is is a single number for each of those directions. Abstracting that idea, a general dimension is just an independent number that is required to specify where something is. The total independence of these numbers is a fundamental key component of the definition; left and right aren’t independent since one’s just the opposite of the other so they constitute the same dimension, but forward and up are truly different things, they’re the difference between pushing the elevator call button and pointing mindlessly in the air.
So that’s a not-extra dimension, the pickle now is what would make a dimensions extra. The regular dimensions we have (listed above) are obvious; if you were aware of a 4th direction you could see, you’d know it, you’d see it, package sizes would read “length, width, height, and extra”. The challenge is therefore to find a way that Nature knows things need 4 (or more) numbers to be properly, fully defined but you only need to know 3 of them. It may be a bit surprising, but in fact we know of many ways this could happen, almost all of which are experimentally testable. An incomplete list might include:
- The extra dimensions could be compact and physically small. This is usually how String theorists describe their extra dimensions, as a place you can technically see and move in, but which is so small and so round that you’ll never really notice.
- The extra dimensions could be non-compact, but warped gravitationally to the point that they look compact. This is kind of like living at the bottom of a very steep valley: you’ll only ever commute along the valley and not up the sides, so if you spent your whole life there, you might stop even thinking of the sides as a place you can go. (This is the Randall-Sundrum model).
- It could be the case that there are loads of compact or non-compact extra dimensions but that the matter we’re made of simply doesn’t talk to or live in them (in physics lingo, we aren’t “coupled” to them). This is like life for stick figure drawings; sure, there are 3 dimensions out there, but sentient stick figures living on a sheet of paper will only ever know about 2 of them unless they perform extremely sensitive gravitational experiments (and even then you might be able to weasel your way out of it with a theory where even gravity doesn’t know about the extra dimensions, in which case it’s up to philosophers to say if they even matter).
Another possibility (one I have been slyly ignoring up until now) is that an extra dimension could be time-like in nature instead of space-like. The keen reader will note that I’ve only been talking about the spatial dimensions up to this point even though it’s widely known that time is considered the fourth dimension. Although mathematically it’s only a simple little minus sign that distinguishes a “timelike” dimension from the “spacelike” ones, the physical consequences are enormous and intimately tied up in the concept of causality. This special relationship between time and causality is the reason it’s unlikely that there are any more than just the one timelike dimension (though not strictly impossible)---until we meet or become time travellers, it’s probably safe to assume there’s just the one time dimension. With that said, time as a fourth dimension does in fact give us insight into how we would see any of the other extra dimensions listed above.
How do we see time? Clearly not the same way we see length or width---instead, we “see” time by reading a time-measuring device, like a watch 1. Wherever we are in space, we can also find out “where” we are in time by looking at a clock, or a watch (hence one of the reasons why it makes sense to think of time as a dimension). Although there are subtle, important ways in which time differs from spatial dimensions, this is not one of them. If there existed one of the extra dimensions listed above---say a tiny circular dimension---then we would identify our spacetime location by marking our length, width, and height with a ruler, our time with a watch, and our extra dimension with a gauge on our other arm. In fact, this is the origin of the “gauge” in the “gauge theories” I’ll be getting to next, it was originally developed in the context of hypothetical extra spatial dimensions for exactly the reason that knowing your position at any point would always mean having to carry an extra gauge around that told you where you were in the extra dimension(s) 2.
So that’s how dimensions and extra-dimensions work, sadly a far cry from the colourful extra dimensions in Star Trek. Even sadder, most of these are testable and have been sought in the lab with disappointing results.
What is a gauge theory, and why is it extra-dimensional?
Now the reason experimental searches for real extra dimensions have failed is that they probably don’t exist---at least not as full-fledged spatial dimensions. If we aim for something a little more modest, it’ll turn out we’re fortunate enough to be graced with many extra dimensions, and what’s more, those dimensions are crucial for our understanding of all of the forces we’ve ever seen.
Instead of asking that everything exists in higher dimensions, try letting just a single small thing feel them, say an electron. Since we’re working on such a small scale now, we’re technically thinking about a quantum mechanical theory, but I’ll save those beautiful details for another time. As described above, in this theory we would imagine electrons go about their business moving freely forward/backward, left/right, up/down, advancing in time, and also tracking a new number with an extra gauge, as in cartoon 1. This is all well and good, but if nobody else can see or feel that extra dimension, we would have a very poor description of Nature because we couldn’t test anything about electrons in a lab, we’d be missing an integral part of their DNA! So to make this program feasible, we also have to suppose that physical measurements of electrons don’t depend on their trajectory through their personal extra dimension. In physics lingo, we call this an internal or gauge symmetry, and we demand our equations be invariant with respect to it. In principle, that’s it! We define a gauge theory to be a theory of some aspect of Nature which is invariant with respect to motion in some special particle’s extra dimension and you take my word for it that that describes a bunch of things in the real world. Ta-Da!
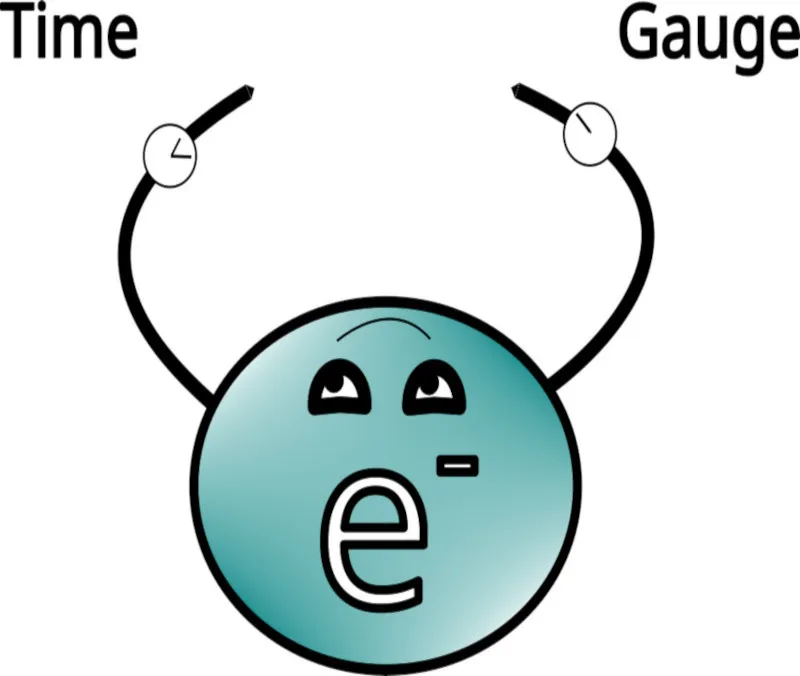 Cartoon 1: A cartoon of an electron with one watch for it to keep track of time, and another to keep track of its extra “gauge” dimension.
Cartoon 1: A cartoon of an electron with one watch for it to keep track of time, and another to keep track of its extra “gauge” dimension.
How Do I Know They Exist?
What’s that? You want some proof? Tsk, you good scientist, you. Well fair enough, if it’s proof you want then I’ve got a doozy for you: gauge theories predict the existence of new particles and we’ve found them. Indeed, remember we’ve let a special type of matter live in an extra dimension and just required our equations to hide it at the end of the day, but what happens in the middle of the day? What happens when two such particles meet up? Imagine two electrons collide as in cartoon 2, their collision will necessarily take place in all the dimensions they both live in, so the kinematics of their collision could easily look completely foreign to us outsiders who aren’t privy to all the details of the interaction (imagine playing billiards but where the balls all have little magnets in them---it would be most infuriating!). Since by design we macroscopic experimenters can never know what’s going on in that extra dimension, we need to introduce a mediator, a third-party who can translate the kinematics of these higher-dimensional interactions into a language we can understand. This has to be a new particle that also feels the electrons’ extra dimension, but we craft it in such as way that its kinematics exactly account for the confusing outcomes we otherwise would have been seeing. So now whenever two electrons interact it’s always from a distance, with this new particle passing the message for them. We call such a mediator a gauge boson for both obvious and bewildering reasons at the non-technical level.
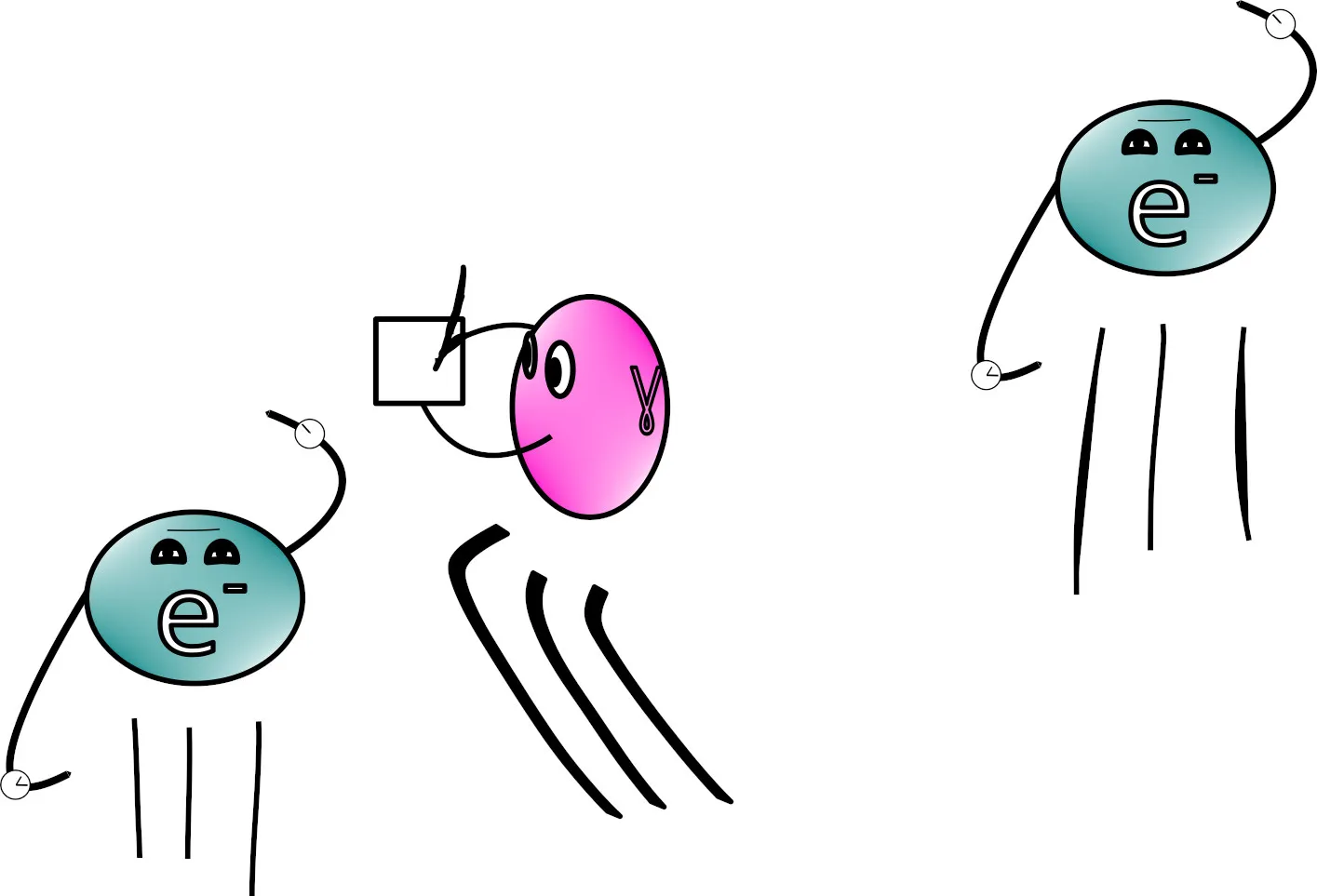 Cartoon 2: A cartoon of a electrons interacting via a mediating photon. The photon is taking note of the first electron’s gauge so it can make sure the interaction goes smoothly, without external observers ever seeing the extra dimension.
Cartoon 2: A cartoon of a electrons interacting via a mediating photon. The photon is taking note of the first electron’s gauge so it can make sure the interaction goes smoothly, without external observers ever seeing the extra dimension.
Gauges and Forces
So the crux of the issue is, if some small particles live in an extra dimension that we can’t see, that can only be the case if there also exists another class of mediator particles that help us make sense of kinematics. But take a step back; the existence of this hidden extra dimension means that when two electrons get near to each other, a gauge boson runs from one to the other to tell it what to do in the extra dimension. De-anthropomorphising a little, a gauge boson can’t just choose to walk from one place to another, it has to get momentum from somewhere, so it’s more like the first electron tosses it to the second. Toss a ball and you’ll move back a little, your friend catches the ball and they’ll also move back a little---it’s almost like you pushed each other or exerted a force on each other from a distance. And finally that’s why a gauge theory represents a theory of a force, particles that live in extra dimensions that we are not allowed to see must interact from a distance through a mediator particle, and the kinematics of those interactions are exactly what we think of as the kinematics of a ranged force 3.
Finally, knowing that a gauge theory can represent a force, the question is “do any known forces fit the mould?” and the answer is “Yes! All of them!” The first and easiest example is Electromagnetism: here the particles are electrons and other electrically charged particles, they feel one extra dimension and the one associated gauge bosons is the photon, the quantum of light. The Weak nuclear force is a gauge theory with two extra dimensions, and particles that feel the Weak force (almost everything) interact with the gauge bosons called the and bosons. The Strong nuclear force is a crazy gauge theory of 8 extra dimensions, and the strongly interacting particles are mediated by a collection of 8 gauge bosons called gluons. Any particle that feels more than one of these forces lives in all of the associated extra dimensions---quarks, for example, feel all of them, so live in 11 extra dimensions (thankfully with no relation to strings)! While the photon was already known when this model was developed, the and bosons were a totally new prediction, and their discovery in the lab a flat-out experimental confirmation of the existence of these extra dimensions 4.
Addendum: Fun Facts
At this point I’ve done my job, I’ve described for you a special type of extra dimension and given you evidence that lots of them actually exist. Now I’d like to go over a few consequences of these theories that lead to fascinating physics.
First, self-interactions. When you have more than one gauge boson mediating the same force, those bosons can talk to and interact with each other, and the result is a very active and messy force. In the case of the Strong nuclear force, this happens to play out in a way that makes it hard to pull particles apart the further apart they are---in other words it is confining, strongly interacting particles have to stick together, which is why quarks only exist in particular combinations that from a distance look like things like protons and neutrons.
Second, broken symmetries. Above I called the Weak nuclear force a gauge theory; this is not quite true. At high energies the Weak nuclear force and the Electromagnetic force are facets of a single 3-extra-dimensional gauge theory called the Electroweak force. At low energies, two of those dimensions get fixed in place by the Higgs particle (a process called “spontaneous symmetry breaking”). That is, all particles moving through those dimensions take a fixed path now, and those paths are parameterized by a measurable quantity, one for each of the fixed dimensions. Those quantities appear as (fairly large) masses for the former-gauge and bosons. Massive gauge bosons are sluggish, they lose the will to do their job, like a water balloon that drained all its water mid-flight. The aptly-named Weak force therefore loses relevance quickly as the distance of interaction increases.
Finally, gravity. Last I checked, gravity is indeed a force, but it is a tricky one. At present, it is technically unknown whether or not it is a gauge theory, but there is good reason to believe it is. Mathematically, gravity can be represented by a theory with 10 hidden extra dimensions (for the nerds: the generators of the Poincaré group) so in principle should be a gauge theory just like the other forces. Unfortunately, as a quantum theory it presents a number of challenges, so more work is needed to determine exactly what the fundamental quantum theory of gravity is (or possibly what the fundamental gravitational theories of the other forces are!).
Footnotes
-
Call it a “chronometer” if you want to sound like a giant nerd. ↩
-
Actually, the origin of gauge theories is a fun time from a theoretical physics perspective. The original gauge theory was proposed by Kaluza and Klein, and was one of the earliest examples of a “unified field theory” (the earliest being electricity+magnetism). The idea was that the world was fundamentally just pure gravity in 1 time + 4 space dimensions, where the extra spatial dimension formed a tiny compact circle. Mathematically, the effect of gravity in the extra dimensions looked (almost) exactly like electromagnetism to the 3 regular dimensions. Unfortunately, the theory also predicted some small effects that were experimentally testable but never seen, so it didn’t work out as a model of the real world, but it’s a beautiful theory nonetheless, and today the mathematical trick they used is named “Kaluza-Klein compactification” in their honour. (A little more reading). ↩
-
Whoa there, okay, for the physicists out there I know that’s not the whole story. Certainly one can construct gauge theories with pure contact interactions (even renormalisable ones, like the Higgs self-interaction), but those theories also necessarily have exchange interactions thanks to the covariant derivative appearing in the kinetic terms. And since the heuristic picture above holds very well for the EM force as the quintessential example of a gauge theory, I’m not losing sleep over the omission. ↩
-
The gluons have not been observed independently because the Strong force is ludicrously complex, but many other related predictions of the model have been verified in the lab, so they’re as good as discovered. ↩