Why Quantum Computing: Probabilities

So computing as we know it requires discrete building blocks, and the quantum world is full of discrete things (even where they’re least expected). This is enough to make a connection between quantum things and computers, but with that bridge established and the topic justified, it’s impossible not to look at the weirdness of the quantum world and wonder if maybe some of it could also be used in computing things.

When you look very closely at the world, to the very small and the very precise, you find a world governed by the laws of quantum physics… and you find that world look a little fuzzier than is comfortable. The concept of a mechanical prediction in the quantum world is reduced from one of certainty to one of probabilities. If you ask where an electron will be at a certain time, the answer comes back “sometimes here, but sometimes there. You’ll just have to check.” How everyone deals with this difficult truth is up to them¹, but once settled down—and with the link to computing already at hand—you just have to ask if this could be used to our advantage in any way.

The answer is (all too fittingly): maybe! But if it is an edge, then that edge comes in two stages. First, the fact that quantum mechanics is probabilistic, and second, exactly how quantum mechanics is probabilistic. Yes that sounds nit-picky but hear me out, they’re meaningfully different.

Probabilities are Cool

What would life be like without a little risk eh? And there’s no risk without chance. Probabilistic things are a fact of life, so it’s a bit surprising that they don’t play much of a role in computers. In fact, real computers are so non-probabilistic that they can’t even produce real random numbers when we need them to, they can only make fake “pseudo”-random numbers².

But theoretical computers have been probabilistic for a long time. Theoretical computer scientists have envisioned all sorts of wild computational schemes and paradigms, but the least exotic of these is just a regular computer with a dash of spicy randomness thrown in. It turns out that this can make it easier to come up with some quick algorithms for things like sorting and testing if an integer is prime, but it is suspected that it really is just a convenience and doesn’t truly add any power to a computer³.

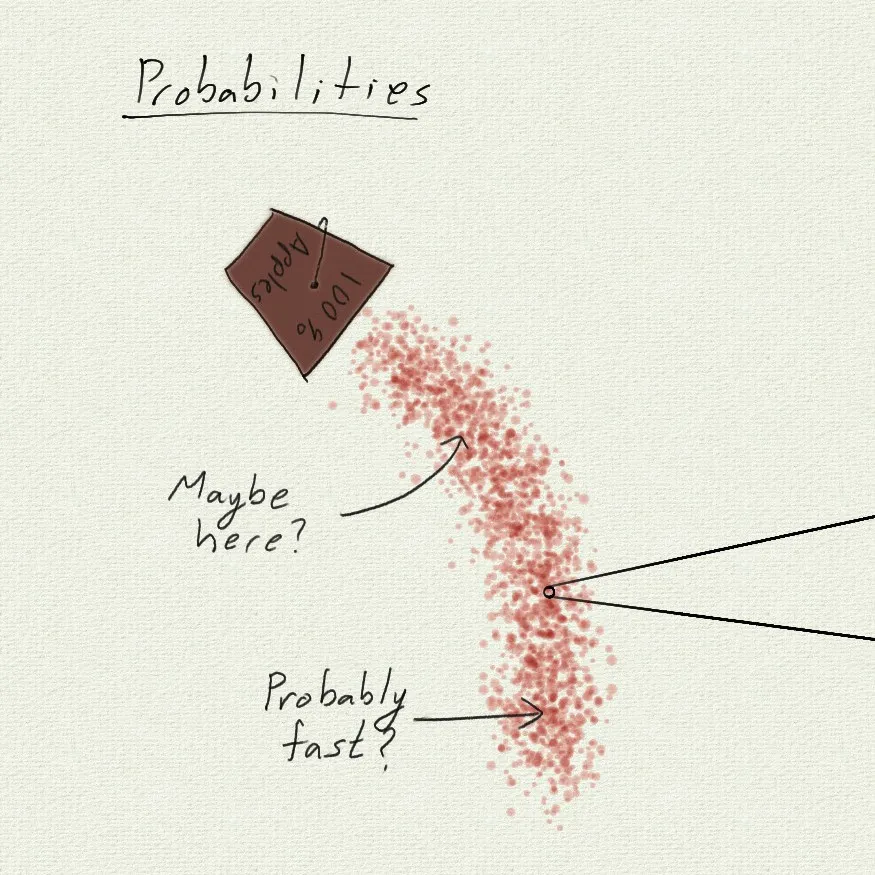
You already have an instinct for probabilities, you can picture a coin flip and think of the 50/50 odds of heads vs tails. Basic probabilities⁴ are super simple: all the things that can happen have a probability of some (positive number) percent, and all the probabilities add up to 100%, because that’s the chance of the future happening.

So far so simple and intuitive…

…but Quantum Mechanics is the Square Root of Probability

Does anyone else remember getting frustrated in school when you took the square root of a number and lost a mark because you forgot to say plus-or-minus \(\pm\) (for example, \(\sqrt{4} = +2\) or \(-2\))? Well behold the consequences of that lost mark: quantum mechanics.

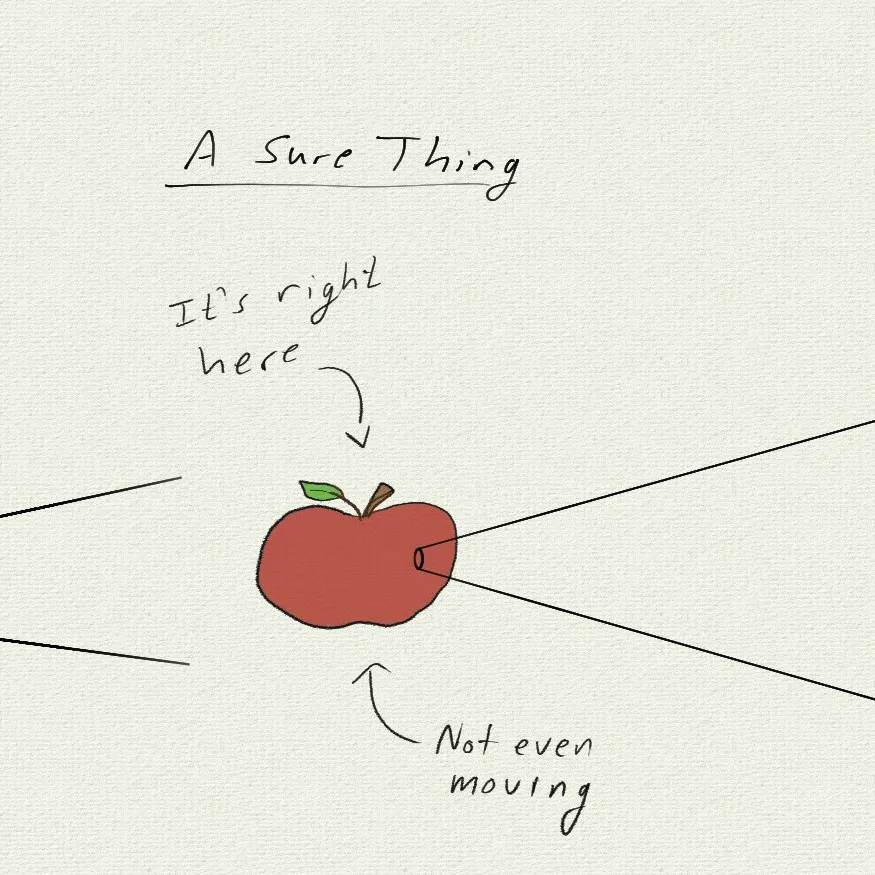
In Newton’s world, the laws of physics speak directly to the things you measure in a lab. Positions, momenta, energies… all directly modelled and directly measured.

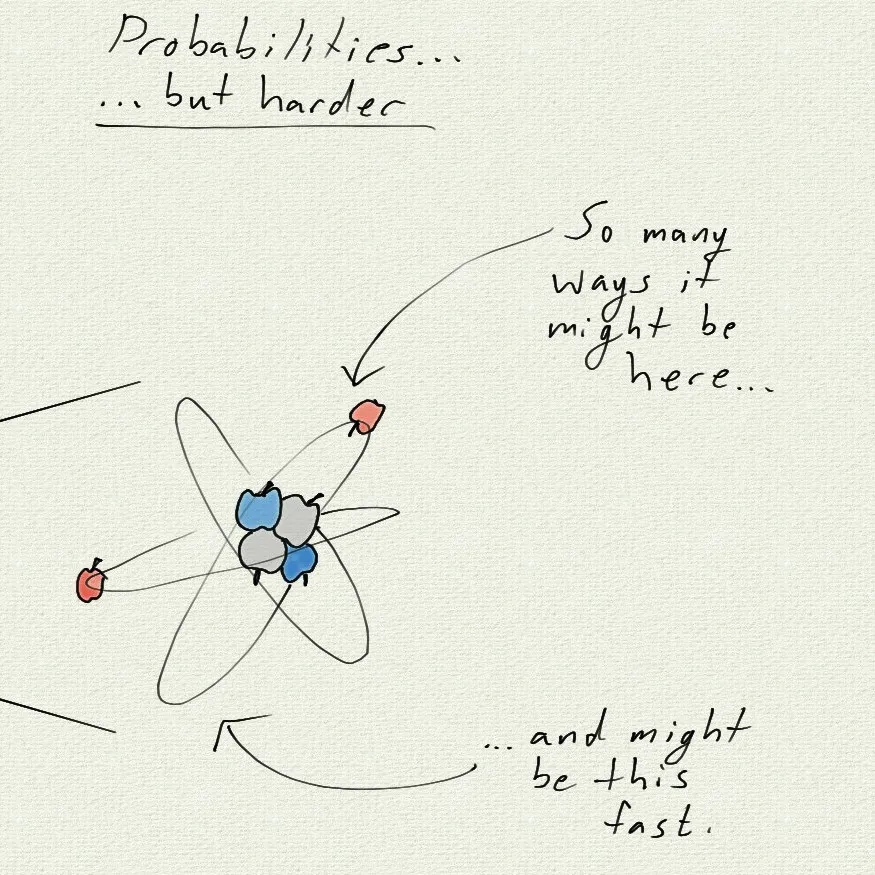
In the thermodynamic world of large collections of Newtonian things, it becomes too much work to follow every individual object (like molecules in a gas, or specks of dust in the air) so instead you take a step back and model probabilities of measuring real physical things. Pressure, temperature, etc. are just averages over distributions of momenta, energies, etc. and we can only guess at an individual particle’s behaviour.

To understand quantum things, you have to take one more step back; your laws of physics no longer directly model probabilities, but the square root of probabilities which we call probability amplitudes.

It gets a fancy name because in quantum mechanics, we take the square root hard. Plus-or-minus is for chumps; quantum physicists craved more and they found it where you’d least suspect. Someone spread a rumour that you can’t take the square root of a negative number, so taking that as a challenge we forcibly broke up the number $-1$ just for fun, just threw caution to the wind and gave it a name. Let me introduce you to $i = \sqrt{-1}$.

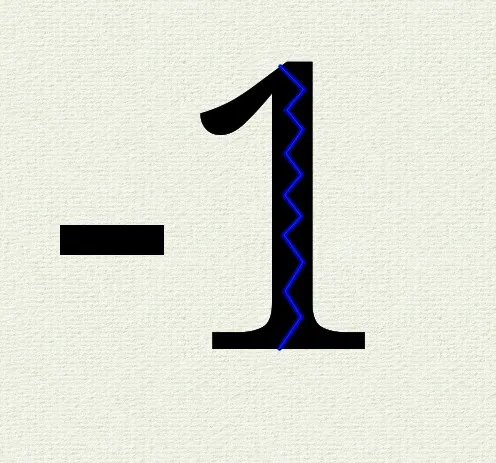
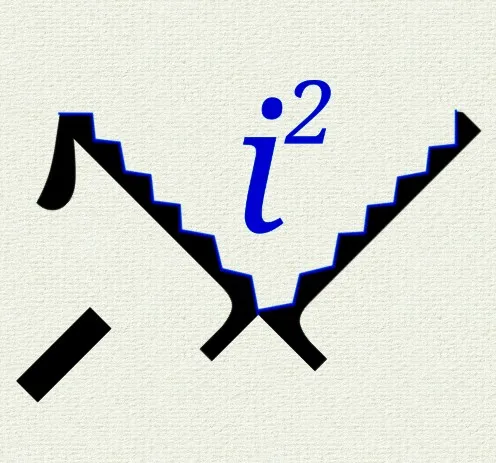
We invented it for fun, but now that we have it look what we can do. It’s still always true that

\[\displaylines{2\times 2 = 4 \\ \text{and} \\ (-2)\times(-2) = 4}\]

but now we can also do this

\[\displaylines{(\sqrt{2} + \sqrt{2}i)\times(\sqrt{2} - \sqrt{2}i) = 4 \\ (2i)\times(-2i) = 4 \\ (-\sqrt{2} + \sqrt{2}i)\times(-\sqrt{2}-\sqrt{2}i) = 4 \\ . \\ . \\ .}\]

In fact, there are now infinite ways to take the square root of a number⁵.

The upshot of this is that since the laws of quantum mechanics describe how probability amplitudes for physical things work, there can be a whole lot of fun stuff going on behind the scenes of the final probabilities we count up in the lab. Or phrased another way, we have a whole lot of freedom with quantum things to influence how they’re going to become probabilities, so now things can get a little less intuitive. Let’s have a look.

Where the magic happens

You’re a mild risk taker, you’ll buy a ticket for a small lottery. 100 total tickets, you buy one and you have a 1% chance of winning, easy peasy.

The quantum version of you does this too and they buy a quantum ticket. Their quantum lottery ticket is very similar to yours, but it’s also a little different. In the quantum world, the very same lottery ticket can come in any number of flavours because there are any number of ways to take the square root of the same regular ticket. I’ll represent this variety with colour. Play with the dial below; the ticket will always read #42 and will always have a 1% chance of winning the lottery, but every different colour is a physically different ticket. I had to truncate the slider for the website, but mathematically there are infinitely⁶ different quantum versions of the same regular ticket.

Now you’re thinking “you know, I could really use this win, I think I’ll get another ticket to increase my odds.” You get a second lottery ticket and bam, your odds of winning just doubled.

Your quantum counterpart has the same thought and they try the same thing…and that’s where their life gets complicated. Quantum tickets add together as amplitudes not as probabilities, so it really matters which versions of the quantum tickets you have. Line two quantum tickets up just right and sure you can double your odds of winning. But line them up wrong and your odds won’t increase that much or even worse, they can vanish altogether! Try it out⁷ (I’ve fixed the first ticket but that’s okay, it’s the difference between the two that matters):

Madness.

For a lottery, that’s a bit of a bummer. But for computing that can be just the ticket, we can potentially use this phenomenon to prop up desired outcomes (like the correct answers to questions) and cancel out the ones we don’t want (the wrong answers).

By the way, this is the Wave part

Actually, everything we’ve just been talking about is the “wave” part of quantum mechanics, what you’ve probably heard as “wave-particle duality,” or “wavefunctions.” When the quantum lottery player added their quantum tickets together, those tickets interfered with each other the way that waves do. When they selected their tickets carefully the tickets interfered constructively and gave a better result, but when they were sloppy, the tickets interfered destructively and they lost all chance of winning.

Mathematically this is really all just about vectors being vectors, but historically the first applications of quantum mechanics were to things that were spatially spread out, and in particular the vectors happened to be solutions to a wave equation, and the name stuck. I’m not complaining, it all sounds pretty cool.

Domesticated Waves

Last time I used light to show a quantum thing being particle-y in the home, and this time I’ll use it to show the same quantum thing being wave-y in the home. This is the classic “3 filter” experiment; I won’t go into too much detail because there are lots of nice explanations online, but the gist is this. Light comes in two species called polarizations, and polarized sunglasses are designed to filter one of them out at a time. You can change which polarization is being filtered by rotating the sunglasses, so two pairs of polarized sunglasses arranged perpendicularly will block out all the light.

Now if light was made up of simple classical particles, that would be the end of the story. If you have a bunch of nickels and dimes and you throw away the nickels first and then the dimes, then you’re just broke, it doesn’t matter what else you do to either of them. But light is made of quantum particles, particles that also act like waves, so we can tinker with them between the filters and the coolest thing happens, light can make it through both of the filters after all! I just did this with ambient light, but you would have seen the same thing shooting one photon at a time at the same setup.

So Reason #2

All quantum particles (and potential replacements for transistors) are also waves of probability amplitude. So a computer made of quantum bits is inherently probabilistic which can be useful on its own, but the physics talks to the square root of that probability, so we can add and subtract things to ensure specific outcomes anyway.

The takeaway here is that thanks to the laws of quantum physics, any quantum transistor comes for free with the option to make it probabilistic (bringing theoretical computer science dreams to life), but also the option to do still more interesting things—potentially powerful things.

---

Pre-emptive Complaints

---

Footnotes